Resampling Schemes
For the list of related C++ classes see Particle Filters.
Contents
1. Resampling algorithms
Both the specific ”particle filter algorithm” to run and the ”resampling scheme” to use can be independently selected in the options structure mrpt::bayes::CParticleFilter::TParticleFilterOptions.
This section reviews four different strategies for resampling a set of particles whose normalized weights are given by ω[i] for i=1,…,N.
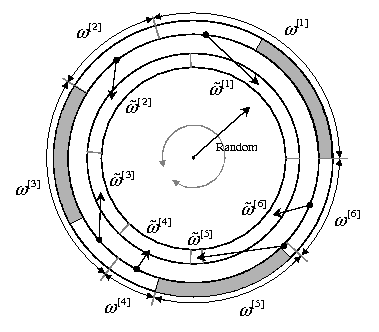
The methods are explained using a visual analogy with a “wheel” whose perimeter is assigned to the different particles in such a way that the length associated to the ”i” ‘th particle is proportional to its weight ω[i]. Therefore, picking a random direction in this “wheel” implies choosing a particle with a probability proportional to its weight.
For a more formal description of the methods, please refer to the excellent paper by Douc, Cappé and Moulines.
1.1 prMultinomial (Default)
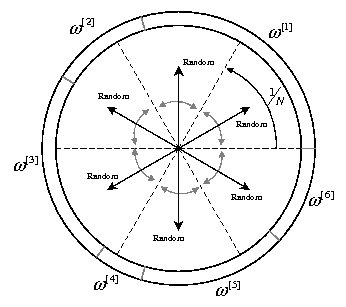
The most straighforward method, where N independent random numbers are generated to pick a particle from the old set. In the “wheel” analogy, illustrated in the figure below, this method consists of picking N independent random directions.
The name of this method comes from the fact that the probability mass function for the duplication counts Ni is the multinomial distribution with the weights as parameters.

1.2 prResidual
This method comprises of two stages. Firstly, particles are sampled deterministically by picking copies of the ”i”’th particle. Then, multinomial sampling is performed with the residual weights
1.3 prStratified
In this method, the “wheel” representing the old set of particles is divided into N equally-sized segments, as represented in the figure below.
Then, N uniform numbers are independently generated like in multinomial sampling, but instead of mapping each draw to the entire circumference, they are mapped to its corresponding partition.
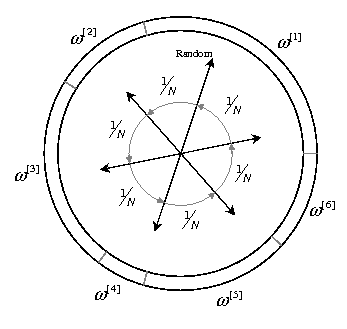
1.4 prSystematic
Also called ”universal sampling”, this popular technique draws only one random number, i.e. one direction in the “wheel”, with the others N-1 directions being fixed at 1/N increments from the random pick.
2. MATLAB version
MATLAB versions of these algorithms have been also published: http://www.mathworks.com/matlabcentral/fileexchange/24968
References
- Douc, R. and Cappe, O. and Moulines, E., “Comparison of Resampling Schemes for Particle Filtering”, Image and Signal Processing and Analysis, 2005.
- Blanco, J.L., Contributions to Localization, Mapping and Navigation in Mobile Robotics, PhD Thesis.